Signed Angle Between 3d Vectors

How to calculate signed angle in range π.
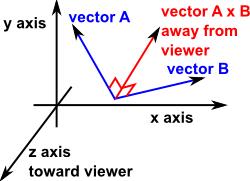
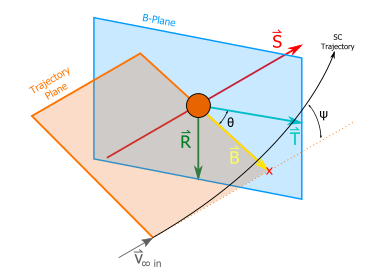
Signed angle between 3d vectors. One special case is the case where your vectors are not placed arbitrarily but lie within a plane with a known normal vector n. For a robust angle between 3 d vectors your actual computation should be. Step by step solution. S length cross product a b c dot product a b angle atan2 s c if you use acos c alone you will get severe precision problems for cases when the angle is small.
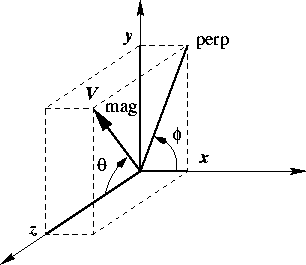
What would be a good definition of a signed angle between the vectors u and v. The smaller of the two possible angles between the two vectors is returned therefore the result will never be greater than 180 degrees or smaller than 180 degrees. For example if u 1 1 and v 1 1 then the angle theta u v would be pi 2 90 degrees since if rotating u. If you imagine the from and to vectors as lines on a piece of paper both originating from the same point then the axis vector would point up out of the paper.
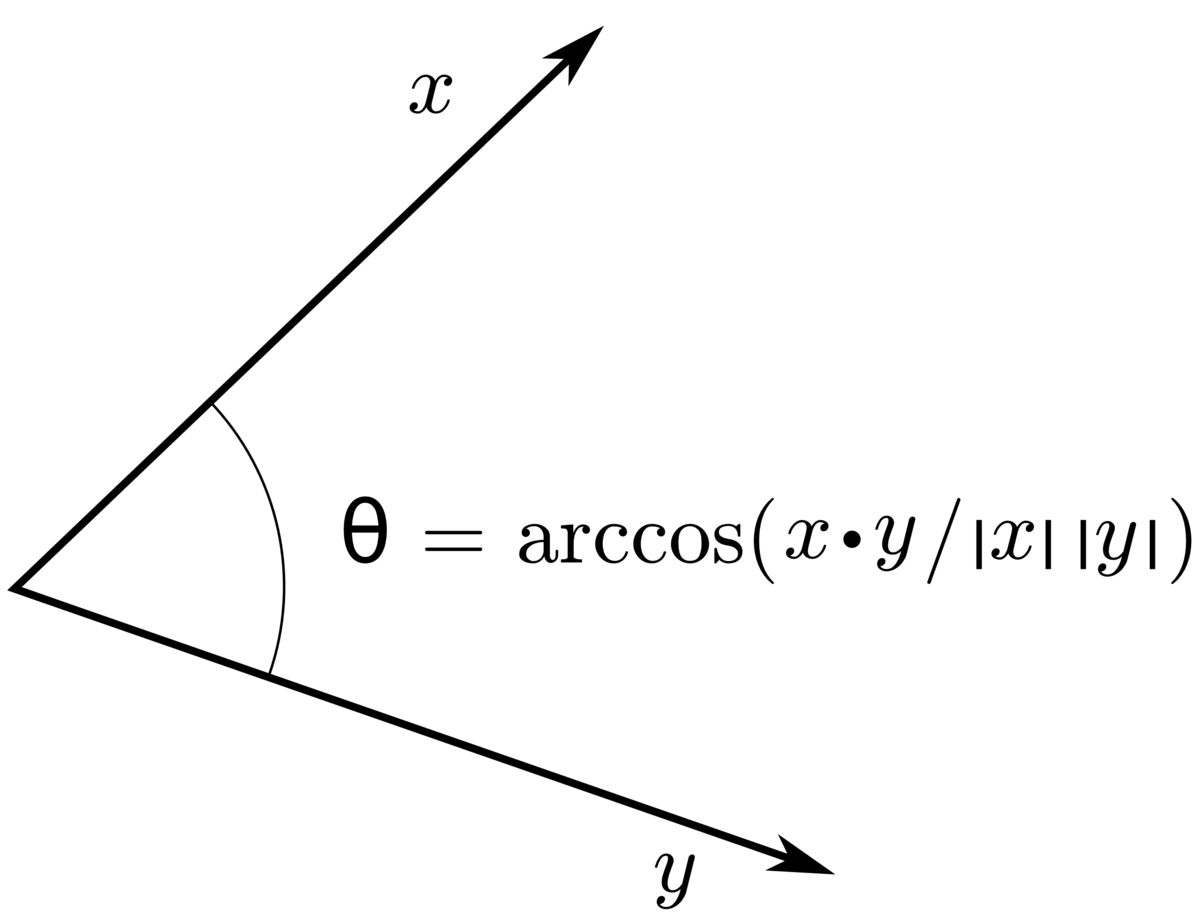
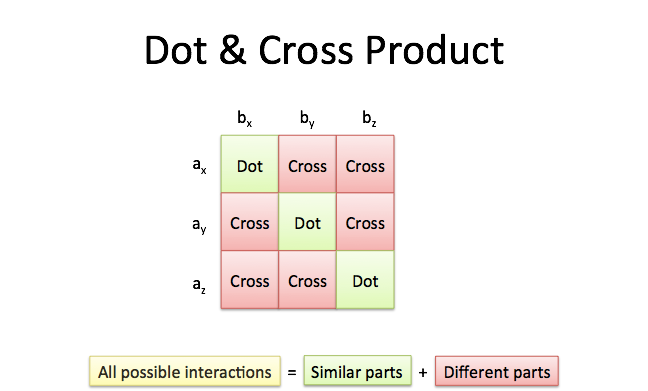
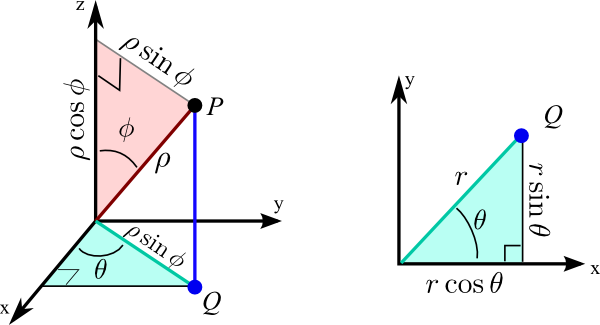
Below are given the definition of the dot product 1 the dot product in terms of the components 2 and the angle between the vectors 3 which will be used below to solve questions related to finding angles between two vectors. In the zero case the axis does not matter and can be anything because there is no rotation round it. Dot x1 x2 y1 y2 z1 z2 between x1 y1 z1 and x2 y2 z2 lensq1 x1 x1 y1 y1 z1 z1 lensq2 x2 x2 y2 y2 z2 z2 angle acos dot sqrt lensq1 lensq2 plane embedded in 3d. Angle acos v1 v2 axis norm v1 x v2 if the vectors are parallel angle 0 or 180 degrees then the length of v1 x v2 will be zero because sin 0 sin 180 0.
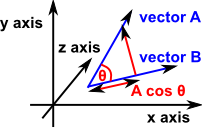
A c o s a b a b gives always positive answer in the range of 0 2 π. Angle between two 3d vectors. π between two vectors in 3d.